【基数変換】小数点以下を2進数表現に変換する方法は簡単

こんにちは、もがちゃんです

コンピュータは、計算が得意と思っていませんか？
コンピュータは、小数が嫌いって知ってますか？

小数点以下の数字を、2進数に変換する方法を知ることで、その答えが見えてきます

小数点以下を2進数に変換する仕組み

小数点以下の10進数を2進数に変換する仕組みを考えるには、2進数がどういう物なのかという事を知っておく必要があります

例えば、2進数(0.101)は、どんな数字なのでしょうか？

2進数(0.101)の各桁の意味を意識すると、以下のように表現することが出来ます
2進数(0.101) = 1/2^1 + 0/2^2 + 1/2^3 = 10進数(0.625)

各桁とも2^nで割っていることに気付くと思います

小数点以下を2進数に変換する方法

小数点以下の10進数を2進数に変換する方法は、変換した小数点以下の10進数に2を掛けた結果の小数部分が「0」になるまで掛けていき変換します

10進数(0.625)を変換した場合の例

0.625 * 2 = 1.25
0.250 * 2 = 0.50
0.500 * 2 = 1.00

この結果の整数部分を上から並べた結果(101)が2進数に変換した結果になります
=> 0.101(2進数)

これだと、分かりづらいので記述方法を変えてみると、以下の図のようになります

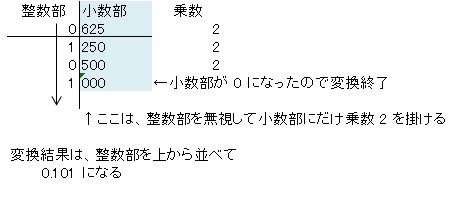
基数変換（小数点以下を2進数へ変換）のまとめ

変換したい小数点以下の10進数に2掛けて、小数部が0になるまで小数部に2を掛け続けた結果の整数部を、上から並べた結果が2進数になります

2進数への変換方法が分かったところで、以下の10進数(0.4)を変換してみましょう
そうすると、以下のように循環してしまいます
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8

これが、コンピュータは、小数が嫌いの理由になります
コンピュータは、0.4という数字をそのままでは、正しく表現出来ないのです
だから、小数の計算には誤差が生じてくるのです